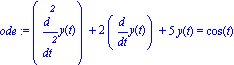
>

>	# (Anything after `#' is for comments. Maple does not treat them as input.) This is a tutorial to some common commands on solving differential equations.

>	with(plots): # Load up the graphic package. End any command with `:' if you don't want to see the output. Otherwise, end it with `;'.

Warning, the name changecoords has been redefined

>	with(DEtools): # Load up another package for differential equations.

>

?dsolve;

>	# Asking question in the form ``?[subject]'' is a very useful tool to learn new commands and techniques.

>	ode:=diff(y(t),t$2)+2*diff(y(t),t)+5*y(t)=cos(t);

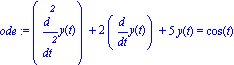
>	dsolve(ode,y(t));

>	ic:=y(0)=10,D(y)(0)=-1;

>	solu:=dsolve({ode,ic},y(t),type=numeric):

>	a:=odeplot(solu,[t,y(t)],0..10,color=black):

>	display({a});# To plot two or more graphs in one plot, use ``display({a,b})'' with ``b'' any another assigned plot variable similar to ``a'' above. You may use plot package, not necessarily the same as ``odeplot'', to generate ``b''.

>	# The following example shows how to solve a system numerically and plot them together against the t-axis.

>	sys := {diff(x(t),t)=y(t),diff(y(t),t)=-x(t),x(0)=1,y(0)=2}; # Put the equations and initial conditions together.

>	syssolu:=dsolve(sys,{x(t),y(t)},type=numeric):

>	aa:=odeplot(syssolu,[t,x(t)],0..10,color=black):

>	bb:=odeplot(syssolu,[t,y(t)],0..10,color=red):

>	display({aa,bb});

>	?dfieldplot; # Find out how to plot direction field.

>	DEplot(diff(y(t),t)=y(t)*(1-y(t)),y(t),t=0..10,{[y(0)=0.5],[y(0)=2]}); #Slope field with solutions.

>	phaseportrait([D(x)(t)=-x(t)-y(t),D(y)(t)=2*x(t)-y(t)], [x(t),y(t)],t=0..20,[[x(0)=1,y(0)=0],[x(0)=3,y(0)=3]],x=-4..4,y=-4..4,stepsize=.05, scene=[x(t),y(t)],linecolour=sin(t*Pi/2)); # Here is another way to do vector field with solutions.

>