|
Population
Dynamics of 2
Preys 1 Predator Models In the process of modeling a food net of one predator, two preys, the behavior of the predator must be carefully considered. For example, the predator may simply hunt for whatever prey it comes to first, or it may be restricted in what prey it can hunt for by the time of day, month, or year, or other environmental factors. These behavioral differences lead to distinct predation considerations in mathematical models, leading to vastly different dynamical phenomena of the system. The predation term models the rate at which the predator consumes the prey according to Holling’s theory on species predation.
The other model, where the
predator must schedule its hunt between two preys leads to two ‘independent’
predation terms. Its behavior is much more complex. It can have equilibrium point, limit cycles
of distinct types, and chaotic dynamics.
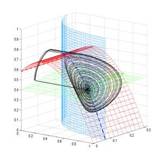
Specifically, this model has a chaotic attractor containing a Shilnikov’s orbit as shown. More
work is needed on the independent predation model to determine if other types
of chaotic behaviors are possible and their ecological implications. Collaborators: Brian Bockelman, Elizabeth Green, Leslie Lippitt, and Jason Sherman, Bo Deng, and Wendy Hines |
Dynamics of
Competition, Predation, Prolificacy of Food Webs In this project we set
out to understand the dynamical forms of competition between two predators, Y, Z,
for a common prey, X, for which one
of the predators, Y, is the prey of a top-predator, W.
The XYW interaction forms a
food chain, whereas the XYZ forms
a food web. A mathematical model is constructed for the study. It is based on two fundamental modeling principles in ecology. The prey is modeled according to the logistic growth model. All the predators are modeled according to the Holling Type II predation functional form. Complex as it is, qualitatively equivalent dynamics can be cataloged according to 3 characteristics of the species: competitiveness, predatory efficiency, and reproductive strength. As examples to illustrate these concepts, we say the predator Z is competitive if all the XY-attractors are unstable in the expanded XYZ-web. We say the predator Y is efficient if the XY-attractor is a stable cycle, and weak if the XY-attractor is a stable equilibrium point. To measure the reproductive strength, we use the ratio of the maximum growth rate of Y to the maximum growth rate of X and call it the YX-prolificacy parameter.
Important
findings are as follows: If both Y
and Z are weak, the classical
Competition Exclusion Principle implies that Y, Z cannot be both
competitive and one must die out. In the case that Z dies out in the XYZ-web,
we demonstrated that it can invade an XYW-chain
where W is a top-predator of Y. The coexistence states in the XYZW-web can be steady state, cycle,
and chaos. In particular, as the ZY-prolificacy
parameter increases, the coexisting state bifurcate from equilibrium points
to periodic cycles to chaotic attractors. Two types of coexisting chaotic
attractors are shown. The one on the right occurs when W is efficient. The one on the left occurs when W is weak. In other words, chaos arises from a
deceptively simple arrangement in the latter case: without Z the XYW dynamics is an equilibrium, and without W the XYZ dynamics
reduces to an XY-equilibrium state
with Z going extinct. Yet, by out
reproducing its competitor Y, Z can invade the chain XYW, and establish a chaotic
coexistence for the expanded web. Numerous
numerical experiments were carried out. More importantly rigorous proofs were
also obtained for the existence of equilibrium, cycle, and chaotic
states. Collaborators: Brian
Bockelman, Elizabeth Green, Leslie Lippitt, and Jason Sherman, Bo Deng, and
Wendy Hines
|
 These
models can be analyzed using techniques such as singular perturbation
analysis, and numerical computation.
These
models can be analyzed using techniques such as singular perturbation
analysis, and numerical computation.
