Notes

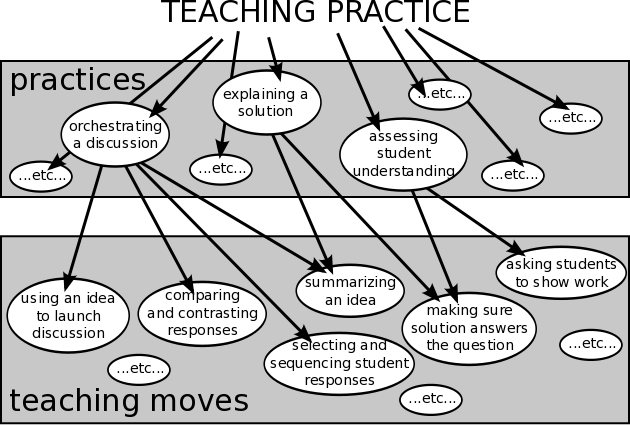
In this course, we view teaching practice as encompassing anything that teaching entails. Teaching practice contains teaching practices: recurring work in teaching that happen across different topics being taught. Teaching moves are actions that happen as a part of a practice. The same move could be used in multiple practices. Here's a schematic depicting this relationship.

Instructional goals

In this course, we view instructional goals as what you want students to accomplish as a result of your instruction. There are many aspects of learning that goals could address. Here, we focus on some goals for mathematics and how to work:

"Collective" refers to building on each others' knowledge as a whole class.

Examples of mathematical "practices" include those from the Common Core Standards of Mathematical Practice.

Norms and routines

Norms are informal and formal rules of interaction that reflect rights, responsibilities, and values. (The interaction could be between students and math, students and other students, students and calculators/compasses/protractors/technology, etc., etc. etc.)

Routines are structures in place to help ensure the norms happen.

Examples of norms

• Contributions are valued and listened to
• Everyone has the right to share their thinking on the problem at hand
• Comments should be connected to what has already been shared
• The way mathematical thinking is communicated should be accessible to others
• An explanation of a proposition should include a clear statement of the proposition
• If a solution uses a procedure learned that day, the procedure should be named and something should be said about why it makes sense to use it.
• Appropriate mathematical terminology should be used

Example of a routine

• After students make appropriate headway on a problem, all students are called to attention, and individual contributions are solicited about the problem.

In this course, a mathematical point includes the mathematical learning goals for an activity, as well as the connection between the activity and its goals -- in other words, what an activity is intended to accomplish mathematically and how it is intended to do so. For example, the mathematical point of an example could be to provoke a common student error in order to develop students’ understanding of a particular concept.

We use the phrase teaching to the mathematical point to talk about these three overlapping aspects of teaching:

• Articulating the mathematical point (i.e., articulating the intended mathematics and how the instructional activity is designed to engage students with it);
• Orienting the instructional activity (i.e., detailing an instructional activity so it is oriented toward the intended mathematics); and
• Steering the instruction (i.e., deploying teaching moves during instruction in an effort to keep students engaged with the intended mathematics).

(These are a summary of the class discussion in Fall 2012 about what was useful when analyzing a task for its mathematical demands/learning opportunities. We noted that "mathematical demands" and "learning opportunities" capture two perspectives on what a task offers: the first emphasizes the mathematical, and the second emphasizes students.)

• Thinking about what students know and need
  • Doing the problem, putting yourself in your past self's shoes and thinking about what your past self would have needed to know
  • Talking with others to get other perspectives
  • Thinking about what students need to know from own experience as well as from a "teacher" perspective.
  • Thinking about what might make a problem difficult -- how a problem might "trick" a student, how a problem might be conceptually difficult. Keeping in mind that different people may interpret difficulty differently.
• Organizing thinking into categories of kinds of mathematical demands/learning opportunities
  • Example categories: procedural, conceptual, math practices
  • Making sure to think about what a task might offer for each of these categories, and what these categories really mean
  • Thinking about what's necessary for "just doing" the task versus what a teacher could do with the task if it were discussed in class

(These are a summary of lessons learned in Fall 2012 about task setup after rehearsals of setting up a problem addressing concavity. I've selected some notecard comments to represent the lessons.)

• It is important to make goals transparent to students, but not make them transparent too early.
• Setting up a task requires more planning than I had anticipated. I would include a problem representation on the board or in a handout for students to refer to.
• I learned that lesson planning requires the organization of all kinds of crazy goals. Making them explicit and clearly identifying how each will be met can be of great assistance when lesson planning.
• I learned that it is critical to be explicit when giving directions and helpful to give students some idea about what they will be asked to do later on. It’s also important to consider how the task is presented given your goals.
• I learned that categorizing specific learning goals is important so that you can effectively meet all of the goals in your lesson by having good organization.
• I learned that tasks take a lot of time, more than I’d like. I also learned that specificity is critical.
• It’s necessary to consider and make clear what students should do with materials.
• It is not as simple as it looks to setup a “simple” task.
• Set up discussion and problem before doing activity.