![number--of-points-in-E- Pr[E] = number of points in S](probability0x.png)
[an error occurred while processing this directive] [an error occurred while processing this directive]

There are 31 educators from the state of Nebraska currently enrolled in Experimentation, Conjecture, and Reasoning. What is the probability that two participants in our class share the same birthday?
![number--of-points-in-E- Pr[E] = number of points in S](probability0x.png)
![]()
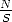 , where S is the
total number of equally likely outcomes in the sample space
and N is the number of
different outcomes giving E.
, where S is the
total number of equally likely outcomes in the sample space
and N is the number of
different outcomes giving E.
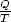 , where T is the
number of times your experiment was repeated and Q is the number of times event E occurred in your experiment.
, where T is the
number of times your experiment was repeated and Q is the number of times event E occurred in your experiment.
![]()
What is the connection between probability and relative frequency? If an experiment is repeated a large number of times, then the relative frequency of a particular outcome will tend to be close to the probability of that particular outcome. We call this the Law of Large Numbers and one of the primary tasks of probability theory is to make this statement more precise and quantitative. In your courses on statistics, you saw one way to do this with the notion of confidence intervals.
Sometimes it is easier to figure out the probability that an event does not happen. Thus, it may be useful to observe: P(E) = 1 - P(N), where P(E) is the probability that the event E does happen and P(N) is the probability that E does not happen. Can you think of three situations when it is easier to determine the probability of an event not happening?
Two cards are selected from an ordinary playing deck. What is the probability that they form a blackjack? That is, what is the probability that one of the cards is an ace, and the other is either a ten, jack queen or king?
The sample space here consists of 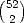 possible outcomes and all
are assumed equally likely.
possible outcomes and all
are assumed equally likely.
Now count the number of ways to get a blackjack. There are 4 ways to have an ace (one from each of the four suits) and then there are 16 ways to get one of the value-10 cards ten, jack, queen, king. Therefore there are 64 blackjack hands.
Hence the probability of a blackjack is
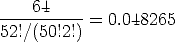
Choose two people at random. What is the probability that they were both born on December 9?
Here the sample space is the set of birthdays: the birthday
of the first person chosen, then the birthday of the second
person chosen. By the Fundamental principle of Counting,
there are 365 × 365
elements in this sample space. We are assuming that all these
choices are equally likely, an assumption based on the
randomness of our selection process and the distribution of
birthdays around the calendar. These are reasonable but not
iron-clad assumptions. The event we are interested in has
exactly one element in it, namely the December 9 and December
9 selection. Therefore the probability is 1/(365)2  7.506 × 10-6.
7.506 × 10-6.
What is the probability of flipping a half-dollar eight time and a heads appearing at least once.
In this problem, the sample space is the set of all possible
sequences of coin-flips, from HHHHHHHH, HHHHHHHT, . . . to
TTTTTTTH, TTTTTTTT. There are 28 equally likely outcomes in this sample
space. Now we are interested in the event that contains
coin-flip sequences with 1, or 2, or ,  r even 8 heads. this
is too many to count, so let’s look at the complement,
the set of coin-flip sequences that have no Heads. There is
only one, namely TTTTTTTT, and so the probability of no heads is 1/28.
The probability of at least one head is 1 - 1/28 =
255/256
r even 8 heads. this
is too many to count, so let’s look at the complement,
the set of coin-flip sequences that have no Heads. There is
only one, namely TTTTTTTT, and so the probability of no heads is 1/28.
The probability of at least one head is 1 - 1/28 =
255/256  0.9961.
0.9961.
The probability of tossing three coins and having all three landing the same is 1/4. What’s wrong with the following dubious reasoning?
When we toss three coins, we know for a fact that two of the coins will land the same, therefore, we only have to get the third one to match. Thus, the probability is 1/2
The fallacy here comes from believing that the sample space we are considering has sample points that are equally likely: Consider having two heads, and desiring to get a third head. There is only one way to get HHH. But consider the probability of having two heads and getting a tail. There are three ways to do this: HHT, HTH, and THH. The probability of getting a third head and not-a-third-head is not 1/2 and 1/2 respectively, it is 1/4 and 3/4 respectively.
This section is adapted from: Instructor Resources and Adjunct Guide for the second edition of The Heart of Mathematics by E. Burger, M. Starbird, and D. Bergstrand. Some of the problems and examples are from A First Course in Probability, by Sheldon Ross.
[an error occurred while processing this directive] [an error occurred while processing this directive]
Last modified: [an error occurred while processing this directive]