Department of Mathematics 203 Avery Hall University of Nebraska Lincoln Lincoln, NE 68588-0323 402-472-3731 (voice) 402-472-8466 (fax)

Question of the Day

A baseball diamond is really a square measuring 90 feet on a side. How far does the catcher have to throw the ball to get it from homeplate to second base?

Key Concepts

1. In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides.
2. In a triangle, if the square of the length of the longest side is equal to the sum of the squares of the lengths of the other two sides, then the triangle is a right triangle.

Vocabulary

1. Theorem In Physics and Mathematics a general proposition not self-evident but proved by a chain of reasoning ORIGIN Greek theorema: speculation, proposition (From the Oxford Compact Dictionary, via askoxford.com)
2. A Pythagorean triple is a triple of positive integers a, b, and c such that a right triangle exists with legs a, b and hypotenuse c. By the Pythagorean theorem, this is equivalent to finding positive integers a, b and c satisfying a² + b² = c². (From mathworld.com)

Mathematical Ideas

Pythagorean Triples

How many examples of whole-number side lengths of right triangles can you find? Is it worth remembering these examples? Is there a formula to generate more such triples? All such triples?

Constructing a Proof of the Pythagorean Theorem

Use the four right triangles in and the small square from your manipulatives kit. Create a single large square with side length equal to the hypotenuse. What is the area of this large square? Now rearrange the shapes into a “fat L” shape whose area is comprised of two squares with areas a² and b².

For many interesting, even animated proofs of the Pythagorean Theorem, see roofs of the Pythagorean Theorem

The most “elegant proof” of the Pythagorean Theorem

Is it legitimate to make a geometric proof of an algebraic statement? Is the Pythagorean Theorem an algebraic statement, or a geometric statement?

This section is adapted from: Instructor Resources and Adjunct Guide for the second edition of The Heart of Mathematics by E. Burger, M. Starbird, and D. Bergstrand.

Sample Worked Problems

Problem 10, page 215, Sand Masting

The backstay is the hypotenuse of a right triangle formed by the deck, the mast and the cable. The base, or leg, of the triangle along the deck has length 50 feet. Therefore, if the mast length is m feet, then 130² = 50² + m². Solving for m, we find that m = 120 feet. Note that the sides of this triangle are in the ratio 5 : 12 : 13 which is very common in these types of problems.

Problem 18, page 216, The practical side of Pythagoras

Using some scrap lumber, (or even some good lumber), carefully measure and create a triangle whose sides are in the ratio 3 : 4 : 5. Since this is patio, we could even create a fairly large triangle, whose dimensions are 3 feet, 4 feet, and hypotenuse 5 feet. Since the sides satisfy the Pythagorean relation 3² + 4² = 5², by the converse to the Pythagorean Theorem, we know it must be a right triangle, with a right angle between the two shorter sides. You can now use this triangle as homemade carpenter’s square to check right angles on your patio. Many scientists believed the ancient Egyptians and Babylonians used a similar idea with knotted ropes for the construction of buildings and monuments.

Problem 19, page 216, Well-rounded shapes

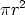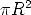The area of the smaller, inner circular disk is . The area of the larger, outer circular disk is . Therefore, the area of the doughnut shaped region inside the outer disk but outside the inner disk is 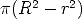However, if we let be the length of the segment that goes from the “North pole” of the inner circle horizontally to the each of the outer circle, then by the Pythagorean theorem, 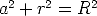. Rearranging, 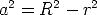and so the area of the doughnut shape is 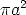. In the second figure, a radius of the shaded medium circle is of length . Therefore the area of the shaded circle is 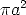also. The two areas are equal.

Problems to Work for Understanding

1. Page 213: Solidifying Ideas: 6,8,9,14,15
2. Page 215: New Ideas: 16,20
3. Page 216: Habits of Mind: 22

I check all the information on each page for correctness and typographical errors. Nevertheless, some errors may occur and I would be grateful if you would alert me to such errors. I make every reasonable effort to present current and accurate information for public use, however I do not guarantee the accuracy or timeliness of information on this website. Your use of the information from this website is strictly voluntary and at your risk.

Last modified: [an error occurred while processing this directive]