[an error occurred while processing this directive] [an error occurred while processing this directive]

On a blank piece of paper (typing paper, no lines) fairly carefully draw the ideal shape that comes to mind when you hear the word “rectangle”. Now measure rectangle and compute the ratio of the longer side (numerator) to the shorter side (denominator). List the ratios from the class.
![]()
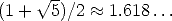 which is the
solution to the equation
which is the
solution to the equation 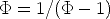
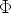 .
.
![]()
Starting with a square  , find the midpoint of the side
, find the midpoint of the side 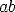 . Extend the
side
. Extend the
side 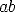 .
Drop the arc of a circle with center
.
Drop the arc of a circle with center 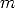 and radius
and radius 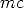 to find the
point
to find the
point  on
the extension of
on
the extension of 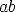 . Now erect a perpendicular to
. Now erect a perpendicular to 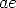 at
at  , and also extend
, and also extend
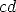 to meet
the perpendicular at
to meet
the perpendicular at 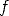 . The resulting rectangle
. The resulting rectangle 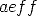 is a Golden
Rectangle.
is a Golden
Rectangle.
Some people say that the proportions of the Parthenon in Athens are the proportions of a Golden Rectangle. What do you think? Somme people say that the Golden Rectangle appears many other places in art, including the Mona Lisa, The Last Supper, and early twentieth-century art by Suerat and Mondrian. What do you think?

This section is adapted from: Instructor Resources and Adjunct Guide for the second edition of The Heart of Mathematics by E. Burger, M. Starbird, and D. Bergstrand.
Why does the equation 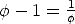 have the same solution as the
equation
have the same solution as the
equation
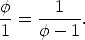
As a solution, suppose that the number 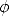 is the solution,
and then multiply both sides of the first equation to obtain:
is the solution,
and then multiply both sides of the first equation to obtain:
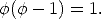
Then divide both sides of the equation by the value 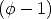 to see that
to see that
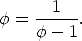
The result is that the value 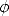 satisfies the second equation too!
satisfies the second equation too!
Since we are only interested in proportions or ratios, we can
set some convenient length to be 1 and measure all other
lengths in terms of this standard. I will take the length of
the vertical side of the original (blue in the figure in the
book) rectangle. Then the length of the longer horizontal
side is 2. The sidelength from the midpoint of the longer
horizontal side is 1. Then the radius of the circle which
swings to extend the rectangle (by the Pythagorean Theorem)
satisfies r2 = 12 + 12 = 2. The radius is 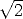 and the
length of the extended side is
and the
length of the extended side is 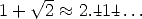 . The ratio of
the long side to the short side is then 1 +
. The ratio of
the long side to the short side is then 1 + 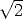 and this is
not a Golden Rectangle.
and this is
not a Golden Rectangle.
Again, since we are concerned with ratios or proportions, we
can choose a convenient side length to be our standard
length. Let the sidelength of the vertical side of the
rectangle be 1, that is the height of the rectangle is 1. Let
the sidelength of the base be b
and assume that  as shown, so that the largest square is removed
from the base as shown. Then removing the square, we are left
with a rectangle of dimensions
as shown, so that the largest square is removed
from the base as shown. Then removing the square, we are left
with a rectangle of dimensions 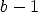 and 1. Then the desired ratio is
and 1. Then the desired ratio is
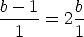
But this is an impossible equation for lengths, since it implies b = -1. So that means b < 1 so the initial rectangle s tall and thin. (Now draw your own diagram to help you visualize the problem solution.) Then removing the square, we obtain
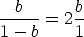
and so solving for b, b = 1/2.
This is not a Golden Rectangle, it is a rectangle twice as
high as it is wide. 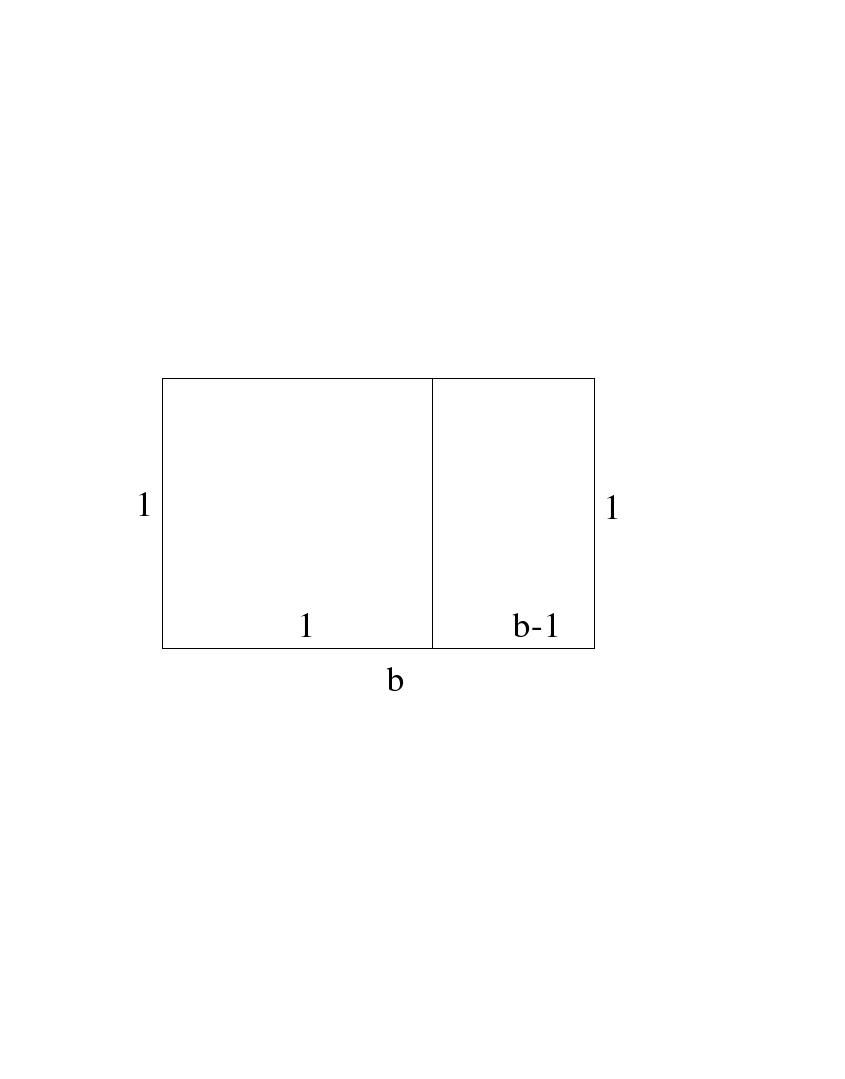
[an error occurred while processing this directive] [an error occurred while processing this directive]
Last modified: [an error occurred while processing this directive]