[an error occurred while processing this directive] [an error occurred while processing this directive]

Question of the Day

How secure is your PIN number for your ATM card? How many 4-character PIN numbers are possible if only the digits 0 through 9 are used? How many 4-character PIN numbers are possible if 26 alphabetic letters and the digits 0 through 9 are used?

Key Concepts

1. Answering questions about probability often reduces to counting how many outcomes are possible, and sometimes counting can be tedious because the number of outcomes is large.
2. However, we have general principles such as the “Product Rule”, also known as the “Fundamental Principle of Counting” that can help us to count in many instances.

Vocabulary

1. A permutation is an arrangement of objects without allowing repetition, and order is important, as in books on a shelf, or letters in a word.
2. A combination is a collection of objects without allowing repetition, and order is not important, as in the members of a committee, or a handful for differently colored marbles from bag, or a collection of numbers for the lottery drawing.

Mathematical Ideas

Warmup with a Simple Problem

How many outcomes are possible if you roll a die and toss a coin. There are twelve outcomes which can be listed in a two-way chart as follows:

The are 6 columns, one for each of the outcomes of the die roll, and two rows, one for each outcome of the coin toss. There are 6 × 2 = 12 total outcomes.

The Fundamental Principle of Counting, or the Product Rule

Consider the following questions:

1. How many outcome sequences are possible if you toss a coin 10 times?
2. How many outcomes are possible if you roll a die 10 times.
3. How many four-character PINS are possible if you can use any digit or letter?

These are counting problems in which order matters and repetition is allowed. We can think of each part of the sequence of outcomes as a step or stage. A certain number of choices are allowed at each step, and the total number of arrangements is the product of the number of choices at each step.

More formally, suppose a process can be completed in two steps, the results of which have no impact on each other. (This is where the repetition is allowed.) If the first step can be completed in m ways, and the second step can be completed in n ways. then the entire process can be completed in mn ways. This is sometimes called the Fundamental Principle of Counting, or the Product Rule. This rule can be quickly generalized to any finite number of steps. and is applied when counting the total number of outcomes of such experiments as tossing coins or rolling dice.

Examples are:

1. When a die is rolled and penny flipped, there are 6 × 2 = 12 possible outcomes.
2. The number of outcomes from flipping a penny 6 times is 2⁶.
3. The number of outcomes from rolling a pair of dice is 6².
4. The number of ways to construct a 5-letter “word”, meaning an arbitrary string of five letters that need not have meaning, is 26⁵ with the English alphabet.
5. The number of possible birth-date selections for a group of 10 people is 365¹0 (assuming no-one was born on February 29).

Permutations

How many outcomes are possible when seating students in a row? Again, there is a sequence of steps to take, seating a student in the first seat, then another student in the second seat, and so on. However, now the number of choices at each stage is changing: If we have a class of 24 students, and we wish to seat students in the first row of 6 seats, then there is 24 ways to choose a student for the first seat, then from the remaining 23 students, 23 ways to choose a student for the second seat, 22 ways to choose a student for the third seat, and so on. Applying the general Fundamental Principle of Counting, there are

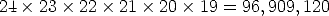
that is, almost 97 million different ways to distinguishably make a row of 6 students from a class of 24. This is a permutation of 24 things taken 6 at a time.

Problem 11, Dealing with Jacks

Here is a solution to a problem from the text: Suppose you deal three cards from a regular deck of 52. What is the probability they will all be jacks?

Here is a probability problem, where we have to count the many possible equally likely outcomes, but which are too many to exhaustively enumerate. However the Fundamental Principle of Counting can help us count the number of possible hands. We can imagine the cards are dealt in sequence, face up, somewhat like blackjack. If we count order in the number of possible hands and then count order in he number of possible all-jack hands, we can divide the number of ordered deals of all jacks, by the total number of equally likely ordered deals to get the desired probability.

The number of equally likely three-card deals (taking distinguishable order into account) is:

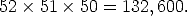
The number of all-jack deals possible is (taking distinguishable order into account) is:

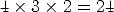
so the probability of an all jack hand is:

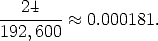
It is possible to work the problem using hands in which the dealt order is not important, somewhat like a hand in bridge, hearts, or pitch. To do so however, would require us to use combination, which I have not addressed directly in these notes, although it is addressed indirectly in the text. It is also possible to work this problem using multiplication of probabilities, finding the probability of a jack on the first card, times the probability of a jack on the second card, times the probability of a jack on the third. While the arithmetic is the same as I did above, it requires some careful thinking about the independence, or lack of independence, in the successive deals of the cards.

Compare this to the Creating New Ideas problem 7, on Counterfeit Bills. You are given 10 $100 bills, and are told 3 of them are counterfeit. You randomly pick three of the bills and burn them. What is the probability that you have burned the counterfeit bills? How are these two problems similar? How are they different? Can you adapt the solution of the first to solve the current problem? Why or why not?

Problem 15, Burger King

You take a summer job making hamburgers. The burgers can be made with any of the following: cheese, lettuce, tomato, pickles, onions, mayo, catsup, and mustard. How many different kinds of burgers can be made.

There are two different ways to work this problem. Here’s the first. For each of the 8 ingredients there are two choices, on or off the hamburger. Hence there are

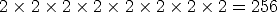
ways to make a hamburger. For the second way to work the problem, we can take 0, 1, 2, 3, 4, 5, 6, 7, or 8 of the 8 possible ingredients and glop them on, order doesn’t matter. Then there are

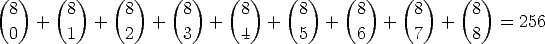
ways to make a burger.

Problem 24, Cranking Tunes

Your car stereo can be programmed to hold six radio stations of your choice. There are nine stations that you really like. How many different ways can you program your six buttons with different collections of your favorite stations? A different ordering of the same six stations counts as different programming.

Here order counts and there are 9 choices for the first button, 8 choices for the second button and so on, counting down six buttons. Hence there are

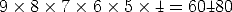
ways to program the buttons.

This section is adapted from: Instructor Resources and Adjunct Guide for the second edition of The Heart of Mathematics by E. Burger, M. Starbird, and D. Bergstrand.

Problems to Work for Understanding

1. Page 566, 6,7,8,10,20,21
2. Page 568, 34,35
3. Page 569, 37

[an error occurred while processing this directive] [an error occurred while processing this directive]

Last modified: [an error occurred while processing this directive]