Roe's Algorithm

In 1998, J. Roe developed an algorithm for computing an integer R(n,m) such that a(n,m) >= R(n,m). Via a sequence of specializations to infinitely near points, Roe shows that any curve of degree d passing through n > 2 points with multiplicity at least m at each point specializes to a curve passing through a single point with multiplicity R(n,m); hence a(n,m) >= R(n,m). (For m not bigger than about n1/2, R(n,m) seems overall to be the best lower bound constructed so far.)

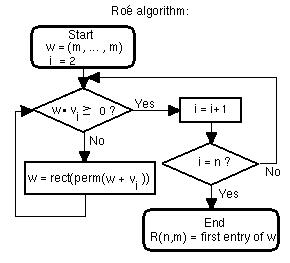
At right is a flowchart for Roe's algorithm for computing R(n,m).
In this flow chart let n > 2 be an integer and let w, v2, ..., vn-1 be elements of the free abelian group Zn with the usual Euclidean inner product, where, in particular:
  • v2 = (1, -1, -1, 0, ..., 0)
  • v3 = (1, -1, -1, -1, 0, ..., 0)
  • ...
  • vn-1 = (1, -1, -1, ..., -1)
Also, for any element x of Zn, perm(x) means to put the entries of x in nonincreasing order, and rect(x) means to replace any negative entry of x by 0.

And here is a web form that implements this algorithm for computing R(n,m) (and other things), based on values of n and m that you enter:
Enter the number n of points here:
Enter a multiplicity m here:
flowchart gif