Practice Quiz 4 covering Chapter 10: Solutions
Instructions: Answer each question, and when required explain your answer. Your explanation must be clear and complete. You may refer to your book, your notes and your homework papers. You may use a calculator.
- [1] (10 points) Problem 12 on p. 646. Also, for each of the parts (b) through (e) of this Problem, determine
the theoretical probability of the event given in each part, assuming that the die and the coin are
fair (i.e, that each side is equally likely to come up).
- (a) The sample space is {1H, 2H, 3H, 4H, 5H, 6H, 7H, 8H, 1T, 2T, 3T, 4T, 5T, 6T, 7T, 8T}.
- (b) E = {2H, 2T}, P(E) = 2/16
- (c) E = {1H, 2H, 3H, 4H, 5H, 6H, 7H, 8H}, P(E) = 8/16
- (d) E = {1T, 3T, 5T, 7T}, P(E) = 4/16
- (e) E = {1H, 2H, 3H, 4H, 5H, 6H, 7H, 8H, 7T}, P(E) = 9/16
- [2] (10 points) Problem 17 on p. 666.
- (a) 4/7
- (b) (2/7)(1/7) = 2/49
- (c) (2/7)(2/7) = 4/49
- (d) 4/7
- (e) (4/7)(1/7) = 4/49
- (f) (4/7)(2/7) = 8/49
- (g) 9
- (h) The marbles were drawn with replacement, since the probabilities for the first stage are the same as those for the second stage. If the marbles weren't put back into the jar after they were drawn, then the probabilities would have changed.
- (i) No. There could be 4 Green, 2 Red and 1 Blue, but we would get the same tree diagram if there were 8 Green, 4 Red and 2 Blue,
or if there were 16 Green, 8 Red and 4 Blue, etc. All we can know for sure are the relative proportions of balls of each color: there are twice as many red as blue, and twice as many green as red.
- (j) (1/7)(1/7) + (2/7)(2/7) + (4/7)(4/7) = 1/49 + 4/49 + 16/49 = 21/49 = 3/7
- [3] (5 points) Problem 5 on p. 687.
- (a) (i) 1/5, (ii) 3/8
- (b) P(R and P) = (4/5)(3/8) = 3/10, P(S and P) = (4/5)(5/8) = 1/2, P(P) = 4/5
- (c) P(R and Q) = (1/3)(1/5) = 1/15, P(S and Q) = (2/3)(1/5) = 2/15, P(R) = P(R and Q) + P(R and P) = 1/15 + 3/10 = 11/30
- (d) P(S|P) = 5/8 = the chance that S happens given that P has happened
- (e) P(Q|R) = P(Q and R)/(P(Q and R) + P(P and R)) = (1/15)/(1/15 + 3/10) = (1/15)/(11/30) = 2/11 = the chance that Q happened given that R has happened
- [4] (5 points) Suppose a screening test for a certain virus is positive 95% of the time for infected people and 2% of the time for uninfected people. Also suppose that 1% of the population is infected.
- (a) Draw a probability tree diagram for the experiment that consists of
randomly picking a person, who may be either infected (i.e., Has the condition) or healthy (i.e., is Free of the condition), and then giving the person the test, which can be either Positive or Negative.
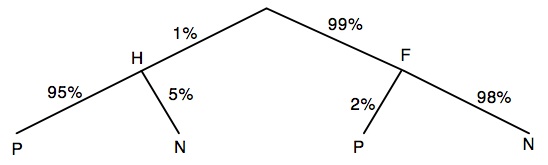
- (b) What is the chance that the person is infected?
P(H) = 1%
- (c) What is the chance that the person tests positive given that
the person is not infected?
P(P | F) = 2%
- (d) What is the chance that the person is not infected given that the test is positive?
P(F | P) = P(F and P)/P(P) = P(F and P)/(P(F and P) + P(H and P)) = (.02)(.99)/((.02)(.99) + (.95)(.01)) = 198/(198 + 95) = 68%
