How in general to set up your integral for computing volume
There are three main methods you can use: horizontal slices;
vertical slices; or
concentric shells. (But concentric shells work only
if you have a volume of revolution, whereas you can always
try the method of slicing. For a figure of revolution, the slices
are perpendicular to the axis of revolution,
so use vertical slices for a horizontal axis
of revolution, and horizontal slices for a vertical axis of revolution.)
When you start a problem, you may not know which method is best.
Just pick one and see what happens!
- If you decide to use vertical slices:
- then you must integrate with respect to x and your integral
will have a dx in it.
- Your integral will be
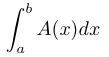 ,
where a = the x-value of the leftmost slice, and
b = the x-value of the rightmost slice. For each x-value, you'll
get a vertical slice whose area A(x) is
a function of x. Here's an example when the volume
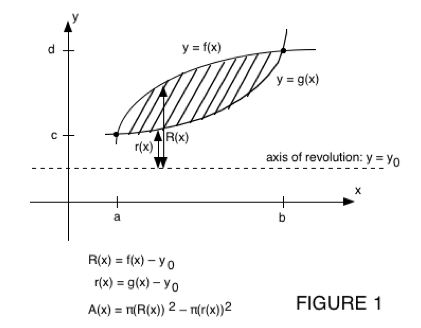
is obtained by revolving a plane region around a horizontal axis
(i.e., the method of vertical washers):
,
where a = the x-value of the leftmost slice, and
b = the x-value of the rightmost slice. For each x-value, you'll
get a vertical slice whose area A(x) is
a function of x. Here's an example when the volume
is obtained by revolving a plane region around a horizontal axis
(i.e., the method of vertical washers):
- If you decide to use horizontal slices:
- then you must integrate with respect to y and your integral
will have a dy in it.
- Your integral will be
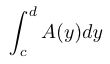 ,
where c = the y-value of the bottom slice, and
d = the y-value of the top slice. For each y-value, you'll
get a horizontal slice whose level is y, and A(y), the area of
the slice, is a function of y. Here's an example when the volume
is obtained by revolving a plane region around a vertical axis
(i.e., the method of horizontal washers). Note that you have to invert
the functions y=f(x) and y=g(x) to express x as functions of y.
That is a disadvantage to using horizontal slices for figures of
revolution revolved around a vertical axis.
,
where c = the y-value of the bottom slice, and
d = the y-value of the top slice. For each y-value, you'll
get a horizontal slice whose level is y, and A(y), the area of
the slice, is a function of y. Here's an example when the volume
is obtained by revolving a plane region around a vertical axis
(i.e., the method of horizontal washers). Note that you have to invert
the functions y=f(x) and y=g(x) to express x as functions of y.
That is a disadvantage to using horizontal slices for figures of
revolution revolved around a vertical axis.
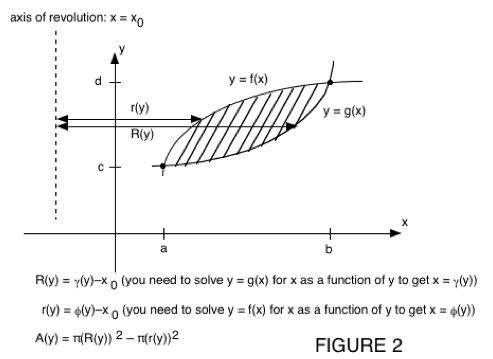
Concentric Shells
- Now suppose you have a problem like that in Figure 1, but you want
to use concentric shells. Then the integral you must use is
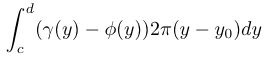 .
Note that this changes the variable of integration, compared to
the method shown in Figure 1,
but you have to invert
the functions y=f(x) and y=g(x) to express x as functions of y.
That is a disadvantage to using shells for figures of
revolution revolved around a horizontal axis.
.
Note that this changes the variable of integration, compared to
the method shown in Figure 1,
but you have to invert
the functions y=f(x) and y=g(x) to express x as functions of y.
That is a disadvantage to using shells for figures of
revolution revolved around a horizontal axis.
- And to use concentric shells with a problem like that in Figure 2,
the integral you must use is
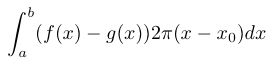 .
Note again that this changes the variable of integration, compared to
the method shown in Figure 2;
using shells for figures of
revolution revolved around a vertical axis
of revolution lets you avoid inverting
the functions y=f(x) and y=g(x). This can be a big advantage!
.
Note again that this changes the variable of integration, compared to
the method shown in Figure 2;
using shells for figures of
revolution revolved around a vertical axis
of revolution lets you avoid inverting
the functions y=f(x) and y=g(x). This can be a big advantage!
- So why would you ever do a Figure 1 problem with shells, or a Figure
2 problem with washers, since then you have to invert y=f(x) and y=g(x)?
See example 3.3 (p. 429); this one has a horizontal axis of revolution
so you'd like to do it like in Figure 1 above, but if you do
you end up needing to break it into two integrals
(this is because the function at the top of the plane region
changes from y=x to y=2-x). If you use
shells, you end up needing to invert y=f(x) and y=g(x)
(which is a disadvantage), but you need only one integral
(which is an advantage).
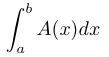 ,
where a = the x-value of the leftmost slice, and
b = the x-value of the rightmost slice. For each x-value, you'll
get a vertical slice whose area A(x) is
a function of x. Here's an example when the volume
is obtained by revolving a plane region around a horizontal axis
(i.e., the method of vertical washers):
,
where a = the x-value of the leftmost slice, and
b = the x-value of the rightmost slice. For each x-value, you'll
get a vertical slice whose area A(x) is
a function of x. Here's an example when the volume
is obtained by revolving a plane region around a horizontal axis
(i.e., the method of vertical washers):
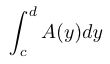 ,
where c = the y-value of the bottom slice, and
d = the y-value of the top slice. For each y-value, you'll
get a horizontal slice whose level is y, and A(y), the area of
the slice, is a function of y. Here's an example when the volume
is obtained by revolving a plane region around a vertical axis
(i.e., the method of horizontal washers). Note that you have to invert
the functions y=f(x) and y=g(x) to express x as functions of y.
That is a disadvantage to using horizontal slices for figures of
revolution revolved around a vertical axis.
,
where c = the y-value of the bottom slice, and
d = the y-value of the top slice. For each y-value, you'll
get a horizontal slice whose level is y, and A(y), the area of
the slice, is a function of y. Here's an example when the volume
is obtained by revolving a plane region around a vertical axis
(i.e., the method of horizontal washers). Note that you have to invert
the functions y=f(x) and y=g(x) to express x as functions of y.
That is a disadvantage to using horizontal slices for figures of
revolution revolved around a vertical axis.
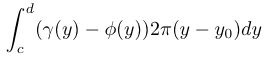 .
Note that this changes the variable of integration, compared to
the method shown in Figure 1,
but you have to invert
the functions y=f(x) and y=g(x) to express x as functions of y.
That is a disadvantage to using shells for figures of
revolution revolved around a horizontal axis.
.
Note that this changes the variable of integration, compared to
the method shown in Figure 1,
but you have to invert
the functions y=f(x) and y=g(x) to express x as functions of y.
That is a disadvantage to using shells for figures of
revolution revolved around a horizontal axis.
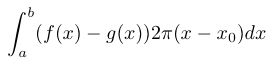 .
Note again that this changes the variable of integration, compared to
the method shown in Figure 2;
using shells for figures of
revolution revolved around a vertical axis
of revolution lets you avoid inverting
the functions y=f(x) and y=g(x). This can be a big advantage!
.
Note again that this changes the variable of integration, compared to
the method shown in Figure 2;
using shells for figures of
revolution revolved around a vertical axis
of revolution lets you avoid inverting
the functions y=f(x) and y=g(x). This can be a big advantage!